With a slew of formals and May Balls being organised by societies to mark the end of the academic year, you couldn’t possibly be more nervous about being judged on tea etiquette. Gowns can be rented for a special day. A white (or black) bowtie could be borrowed from that dependable friend. But what if you strike up a conversation with a Cambridge don (with possibly an OBE to boot!) at one of these events and don’t know whether to add the tea or milk infusion first to the sparkling bone-china. There ends your reputation. This question is so sensitive that celebrated English tea connoisseur (and writer) George Orwell famously described himself as a tea-before-milk person. Here we try to assuage such fears by approaching this quintessential question from the perspective of a mathematician. Does it really matter whether you add tea or milk first and can your taste buds detect such an order? 

8 cups of tea were to be presented to a subject with 4 of them having tea poured first.

The story goes that on a particularly unremarkable summer afternoon (probably not very different from today) in Cambridge in the 1920s, Caius alum, Ronald Fischer devised his eponymous test. 8 cups of tea were to be presented to a subject with 4 of them having tea poured first while the other 4 having milk first in various concentrations. The subject would be told in advance that she would be asked to taste eight cups and that there would be four of each kind.

There exists 8!/(4!4!)=70 distinct possible orderings of these cups. By telling the subject in advance that there are four cups of each type we guarantee that the answer will include four of each. Next, we compare whether the subject can detect any better than random chance which is 4 out of the 8 cases or exactly 50%. We can compute the probability of a sample of correct detections of tea or milk first using Fischer’s exact test or a hypergeometric test (not the binomial test, since the events are no longer independent).

This is compared with the so-called p-value to the null hypothesis. In this case, the null hypothesis is: The lady is not right any more than random chance would allow.

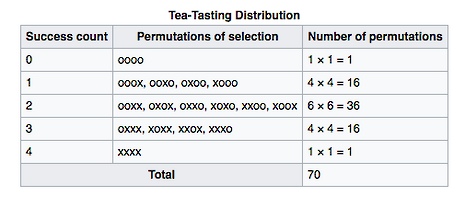
In a hypothetical scenario, in which 8 cups were offered and the subject guessed correctly 6 times, the p-value is approximately 24% (17/70). In a purely randomised guessing environment, the subject would be expected to guess as well as she did 24% of the time. Usually, we consider a significance level of 0.05 (5%) as an informal rule to disprove the null hypothesis. Therefore, the above p-value of 24% is considered insignificant. On the other hand, a greater deviation from randomness (such as guessing all tea cups right or wrong) would be described as significant, and a significant deviation would have the function of rejecting the null hypothesis.

The null hypothesis is: The lady is not right any more than random chance would allow.

In an actual scenario, an algae researcher (phycologist) named Dr Muriel Bristol working in Hertfordshire took Fischer’s test and legendarily got all 8 cases correct. The p-value for this test result for Dr Bristol was 1/70, or 1.4%: a 'significant value', in terms of statistics. In doing so, she beat Sir Fisher’s stated odds, and he rejected his null hypothesis.

It is not possible to prove that she would never be wrong because if a sufficiently large number of cups of tea were offered, a single failure would disprove such a hypothesis. However, a test that she is never right can be disproven, within a certain margin of uncertainty, given the number of cups offered. And that is what we did here.

Bread and Rutter: The UL Tearoom

Finally, we pour a bit of chemistry for taste to the above resolution to explain why this taste change occurs at all. It appears that the degree of denaturation of proteins with heat is what causes the taste difference in pour order which we proved above could be distinguished by at least one person, at least some of the time