Alice takes a COVID-19 test, and it comes back positive. Does Alice have COVID-19?

The answer is that we don’t know for sure, because COVID-19 tests, like all medical tests, are not perfectly accurate. It is possible to test positive and not have COVID-19, and similarly one can test negative despite being infected.

There are several types of COVID-19 test, but suppose Alice takes a test that has a probability of 95% of giving a positive result if someone is infected (this is called sensitivity) and the same probability of correctly giving a negative result if someone is not infected (this is called specificity). (Note that these numbers have been made up for this example.) Can we now answer the question: what is the probability that Alice has COVID-19, given that she tested positive?

In fact, we can’t, not without more information. If Alice lives with ten roommates who are all infected and has a high temperature and no sense of smell, then we would think it very likely that Alice has COVID-19; if Alice is completely symptom-free and lives in the Pacific island nation of Palau, which has never recorded a case of the disease, we would assume that she almost certainly got a false positive.

It is possible to carry out reasoning like this in a more rigorous way, using something called Bayes’ theorem. Named after an 18th-century English clergyman called Thomas Bayes, this simple equation can be used to answer questions such as Alice’s dilemma, and underpins much of modern science. Using this rule can often produce counterintuitive results, as we will soon see.

Mathematically, the rule looks as follows, where P(A|B) means “the probability of event A occurring given that event B has occurred”.

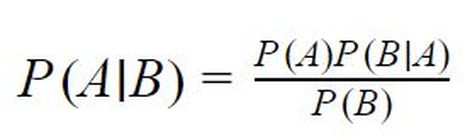
It is easiest to explain this formula by working through the calculations in the case of Alice.

To get a more accurate estimate of the probability that Alice has COVID-19, more information about her is needed. Suppose we are told that Alice is in London on 19 February 2021; the Office for National Statistics survey estimated that 1 in 100 people there was infected with COVID-19 on that date. If we did not know about Alice’s positive test result (or anything else about Alice), this would be our estimate of the probability that Alice has COVID-19: 1%. This initial estimate is called our prior probability (often just called the prior).

When we take Alice’s positive test into account, we know that our estimate for the probability of her being infected will rise, but by how much? We can use the formula directly, but perhaps the easiest way to think about this is to imagine a large sample of people in London, say one hundred thousand, and suppose they all took a COVID-19 test.

Of these 100 000 people, 1 000 (i.e. 1% of them) would be expected to have COVID-19, with the remaining 99 000 infection-free. Since we have assumed that our test has 95% sensitivity and 95% specificity, this means that 95% of the 1 000 and 5% of the 99 000 would have a positive result. This means that we would expect to have 5 900 positive test results, of whom 950 would be from people with COVID-19. Therefore the probability of someone with a positive test result (such as Alice) having COVID-19 is 950 divided by 5 900, or about 16%. This updated estimate for the probability we want to measure, based on new information, is called the posterior distribution.

This is surprisingly small! Even though most tests give accurate results, because the probability of someone having COVID-19 is very small, false positives actually make up the majority of positive test results. This is sometimes called the base rate paradox, and has many applications, all of which stem from the same issue: failing to note that the prior probability of an event (the base rate) is small in comparison to the chance of a false positive. (In reality, most COVID-19 tests have higher specificity and sensitivity than the imaginary test described in this article.)

“Even though most tests give accurate results, because the probability of someone having COVID-19 is very small, false positives actually make up the majority of positive test results”

The beauty of Bayes’ theorem is that it can be applied again and again every time we have more information. For example, if we were told that Alice has a new, continuous cough, then because the probability of someone with COVID-19 having a cough is higher than the probability of someone without the disease having a cough, our posterior probability of Alice having COVID-19 would be higher than our prior probability.

A simpler example might be to imagine if Alice took a second test after her first, and it also came back positive. What would our estimate for the probability that she is infected be now? We do essentially the same calculation as before but take the prior probability to be 16% instead of 1%. The posterior probability becomes:

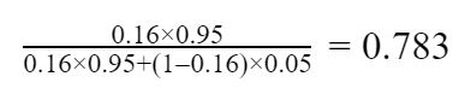
So it is now likely that Alice is infected; our posterior probability is 78%, or about four-fifths. If Alice kept taking tests and they kept coming back positive, our estimate for the probability that she is infected would continue to rise, getting closer and closer to 100%, but never quite reaching it (since it is always theoretically possible that all of her tests results were false positives).

Bayesian methods are now used throughout science, particularly in artificial intelligence and machine learning. Bayes’ theorem can be extended and generalised using more advanced mathematics (for example, it can also be used to study continuous probability distributions), and Bayesian statistics is one of the most common approaches to statistics today. It is remarkable how such a simple equation can produce such unintuitive results, and help us to understand the world better.