Let’s look at this for the most ubiquitous language: English. (Although, this should work for any Latin script language like French or German. The means and standard deviation will, however, be possibly different.)

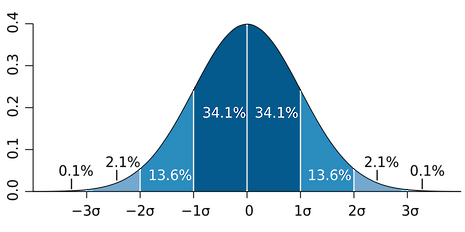
Let us assume a Gaussian distribution for the number of words with respect to the number of letters per word. Here is what a normal distribution looks like:

By simply eyeballing through passages we can estimate that most probable word length is 5 letters. Now, to estimate the standard deviation, we can notice that 66.67% of words are of lengths between 3–7 words. Thus 1σ = 2 letters. This is a rough estimate based completely on eyeballing approximations.

Now to calculate the maximum possible words:

We know that the longest word in the English Language is pneumonoultramicroscopicsilicovolcanoconiosis. A 42 letter Leviathan which is a kind of lung disease due to inhaling ash particles (‘silicon’). This word is a good 18.5 standard deviations away from the mean! This means that the likelihood of finding a word this long is close to zero.

However, if we want a strict mathematical limit we have (based on largest word length):

26×26…(42 times)=26^(42)=2.6846064×10^(59)

A 59 digit number! It could obviously go higher if using 100 or 150 letter words comes into vogue. (I hear that the Germans already do this!)

A 100% (total number) of possible words would be about 103,503,945. Or around 100 million total words.

This doesn’t really appear ‘realistic’. So let’s see how we can arrive at that figure. First, we note, that since the right side of the Gaussian can extend asymmetrically much more than the left side which is bound by 1 letter words (Zero and negative letter words don’t exist!). However, since the likelihood of words greater than 10 is very low, we can for current purposes ignore them. ( This is an approximation used to make my life easier to solve this. We could as well use MATLAB to plot a skewed Gaussian but I’m reasonably confident the percentage error won’t be too significant.)

Therefore about 67% of words are:

26×5×26+26×5×26×5+26×26×5×26×5+26×26×5×26×5×26+26×26×5×26×5×26×5=69006080

The above accounts for the frequency of vowels in all words of length 3–7 as well. That is about 69 million. A 100% (total number) of possible words would be about 103503945. Or around 100 million total words.

Tea first or Milk first

Dictionary Facts - Oxford English Dictionary says that they have around 414,800 ‘entries’ defined. These are the words that we most use on a day to day basis. The culturomics folks came up with these numbers in a paper in Science in 2011. Using this technique, they estimated the number of words in the English lexicon as 544,000 in 1900, 597,000 in 1950, and 1,022,000 in 2000 – Quantitative Analysis of Culture Using Millions of Digitized Books (they only looked at 4% of English-language books in Google’s corpus).

At Wordnik, we have knowledge of nearly 8 million wordlike strings. Many of these are lexicalised phrases, some are in-jokes, some are names or foreign-language terms. That is still about 10% of total potential word strings which could be formed