When we look at a beautiful flower, we are not always consciously aware of what exactly is aesthetically pleasing about it. More often than not, however, it is symmetry that catches the eye. Indeed, most natural objects tend to develop according to patterns, a tendency which mathematicians readily exploit in order to create theoretical models of the world around us, most easily in one, two, or three dimensions. Yet, what about objects in between dimensions; those that cannot be represented by classical Euclidean geometry? This is where fractals come into play. Derived from the Latin ‘fractus’, meaning fragmented, fractals are mathematical objects with a non-integer dimension. Such mathematical objects can be self-similar ad infinitum - as one magnifies a certain part of the fractal, the figure of the overall fractal will be seen. Imagine, for example, the Koch curve: a six-tip snowflake, with each tip resembling the original snowflake, and so on.

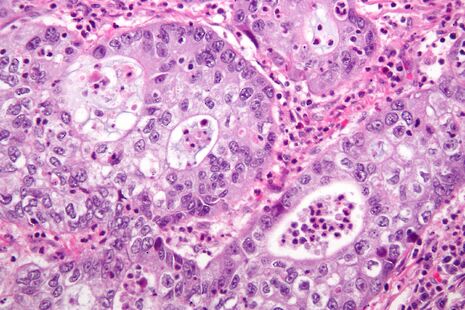
Clearly, however, natural fractal objects are composed of discrete units and are not infinitely divisible. The fractal pattern must end somewhere. As in all models of nature, herein lies some difference between the mathematical and the natural. This is corrected for in practice by the concept of statistical self-similarity: when the statistical properties of the segments of an object are proportional to the statistical properties of the whole. Statistically self-similar models are ubiquitous not only externally, but internally too. Examine our lungs, blood vessel networks and even our heartbeats, and you will find fractal trees. Beyond mere observation, studies are beginning to show that fractal geometry, our vocabulary of irregular shapes, can be useful for describing the pathological architecture of tumours; in particular, for yielding insights into mechanisms of the genesis of the blood vessels that will feed their ceaseless appetites.

“The mammary ducts and glands of the breast adhere to a perfect fractal geometry”

Tumours induce the growth of their own blood vessels (angiogenesis) through the secretion of various growth factors. It is thought that the emergent capillary supply provides essential nutrients, allowing for tumour expansion. Little wonder then, that sustained angiogenesis is one of Hanahan & Weinberg’s seminal ‘hallmarks of cancer’. Microscopically, what is interesting about tumour blood vessels relative to their ‘normal’ counterparts are their dilated, distorted shapes. They illustrate a morphology underpinned by a fractal model, and this can be demonstrated quantitatively: in 2000, Baish & Jain observed that blood vessels in the tumours of mice had higher fractal dimensions than the mice’s normal arteries and veins, and were more twisted than normal vessels, having many smaller bends upon each larger bend. In sum, a statistical fractal model was the best-suited for the irregularly shaped tumour vasculature.

Furthermore, the remit of fractal geometry within oncology may also permeate the inception of malignancies themselves. For example, much like the other aforementioned human anatomical systems, the mammary ducts and glands of the breast adhere – in normality – to a perfect fractal geometry. This is devastated by breast cancer. Studies such as those of UCL’s Michael Baum suggest that such a loss in different breast tissues could be an early, but committed, step in oncogenesis.

Being able to quantify the irregular structures that are present in tumours both gives us clues to their origins, and helps us to clarify why treatment is still so frustratingly difficult. Whether fractals will ultimately find a place in the oncologist’s toolbox, however, awaits more controlled comparisons with conventional pathological procedures